By Agustín Mista

Random property-based testing (or random testing for short) is nothing new, yet it is still a quite hot research field with many open problems to dig into. In this post I will try to give a brief explanation of our latest contribution on random testing published in the proceedings of the 2018 Haskell Symposium, as well as some use cases of DRAGEN, the tool we implemented to automate the boring stuff of using random testing in Haskell.

The key idea of random testing is pretty simple: you write the desired properties of your system as predicates, and try to falsify them via randomly generated test cases. Despite there are many, many libraries that provide this functionality, implemented for a bunch of programming languages, here we will put the spotlight over QuickCheck in Haskell. QuickCheck is the most prominent tool around, originally conceived by Claessen and Hughes almost twenty years ago. If you haven’t heard of it, I strongly recommend checking the original paper but, being more realistic, if you’re reading this you likely know about QuickCheck already.

In this post I will focus on using QuickCheck as a fuzzing tool. Essentially, fuzzing is a penetration testing technique that involves running a target program against broken or unexpected inputs, asserting that they’re always handled properly. In particular, I’ll show you how to use existing Haskell data types as “lightweight specifications” of the input format of external target programs, and how we can rely on meta-programming to obtain random data generators for those formats automatically. In the future, the Octopi project will apply this technique to evaluate and improve the security of IoT devices.

QuickCheck + fuzzing = ♥

Software fuzzing is a technique that tries to reduce the testing bias by considering the target program as a black-box, meaning that we can only evaluate its correctness based on the outputs we obtain from the inputs we use to test it.

This black-box fashion of testing forces us to express our testing properties using a higher level of abstraction. For instance, one of the most general properties that we can state over any external program consists in checking for succesful termination, regardless of the inputs we provide it. We can express such property in QuickCheck as follows:

prop_run :: Arbitrary t => String -> (t -> ByteString) -> t -> Property
prop_run target encode testcase = monadicIO $ do
  exitCode <- run $ shell target $ encode testcase
  assert (exitCode == ExitSuccess)

shell :: String -> ByteString -> IO ExitCode
shell cmd stdin = do
  (exitCode, _, _) <- readProcessWithExitCode cmd [] stdin
  return exitCode

From the previous property, we can observe that we need a couple of things in order to test it:

1. A shell command target to execute.
2. A data type t describing the structure of the inputs of our target program.
3. A random generator for t, here satisfied by the Arbitrary t constraint.
4. A function encode :: t -> ByteString to transform our randomly generated Haskell values into the syntactic representation of the standard input of our target program.

Aditionally, note that here we decided to use the standard input of our target program as interface, but nothing stops us from saving the test case into a file and then running the target program using its filepath. In both cases, the idea is essentially the same.

Then, we can test for instance that the unix sort utility always terminates successfully when we run it with randomly generated Ints. The first step is to define an encoding function from [Int] to ByteString:

-- We simply put every number in a diferent line
encode :: [Int] -> ByteString
encode ints = ByteString.fromString . unlines . map show

The next requirement is to have a random generator for [Int]. Fortunately, this is already provided by QuickCheck in the following Arbitrary instances:

instance Arbitrary Int
instance Arbitrary a => Arbitrary [a]

With both things in place, we can check that we generate and encode our data in the right way in order to call sort:

ghci> encode <$> generate arbitrary >>= ByteString.putStr
-16
19
-28
-16
9
26
2
9
9

Finally, we can simply test sort by calling:

ghci> quickCheck $ prop_run "sort" encode
+++ OK, passed 100 tests.

In many scenarios, it might also be interesting to use an external fuzzer to corrupt the generated ByteStrings before piping them to our target program, looking for bugs related to the syntactic representation of its inputs. For instance, we could consider using the deterministic bit-level fuzzer zzuf from caca labs:

$ echo "hello world" | zzuf
henlo world
$ echo "int foo() { retun 42; }" | zzuf --ratio 0.02
int goo() { return 22; }

Then, we can modify our original property prop_run in order to run zzuf in the middle to corrupt the randomly generated test cases:

zzuf :: ByteString -> IO ByteString
zzuf stdin = do
  (_, stdout, _) <- readProcessWithExitCode "zzuf" [] stdin
  return stdout

prop_run_zzuf :: Arbitrary t => String -> (t -> ByteString) -> t -> Property
prop_run_zzuf target encode testcase = monadicIO $ do
  exitCode <- run $ shell target <=< zzuf $ encode testcase
  assert (exitCode == ExitSuccess)

Which will produce corrupted outputs like:

ghci> encode <$> generate arbitrary >>= zzuf >>= ByteString.putStr
-18
-19
3:�
-02*39$34
30
22
-:)
"9
;y

As simple as this testing method sounds, it turns out it can be quite powerful in practice, and it’s actually the main idea behind QuickFuzz, a random fuzzer that uses existing Haskell libraries under the hood to find bugs in a complex software, spanning a wide variety of file formats.

Moreover, given that QuickCheck uses a type-driven generational approach, we can exploit Haskell’s powerful type system in order to define abstract data types encoding highly-strutured data like, for instance, well-scoped source code, finite state machines, stateless communication protocols, etc. Such data types essentially act as a lightweight grammar of the input domain of our target program. Then, we are required to provide random generators for such data types in order to use them with QuickCheck, which is the topic of the next section.

Random generators for custom data types

In the previous example, I’ve shown you how to test an external program easily, provided that we had a QuickCheck random generator for the data type encoding the structure of its inputs. However, if we are lucky enough to find an existing library providing a suitable representation for the inputs of our particular target program, as well as encoding functions required, then it’s rarely the case for such library to also provide a random generation for this representation that we could use to randomly test our target program. The only solution in this case is, as you might imagine, to provide a random generator by ourselves or, as I’m going to show you by the end of this post, to derive it automatically!

As I’ve introduced before, whenever we want to use QuickCheck with user-defined data types, we need to provide a random generator for such data type. For the rest of this post I will use the following data type as a motivating example, representing 2-3 trees with two different kinds of leaves:

data Tree
  = LeafA
  | LeafB
  | Node Tree Tree
  | Fork Tree Tree Tree

The easiest way of generating values of Tree is by providing an instance of QuickCheck’s Arbitrary type class for it:

class Arbitrary a where
 arbitrary :: Gen a
 ...

This ubiquitous type class essentially abstracts the overhead of randomly generating values of different types by overloading a single value arbitrary that represents a monadic generator of Gen a for every type a we want to generate. That said, we can easily instantiate this type class for Tree very easily:

instance Arbitrary Tree where
 arbitrary = oneof
   [ pure LeafA
   , pure LeafB
   , Node <$> arbitrary <*> arbitrary
   , Fork <$> arbitrary <*> arbitrary <*> arbitrary
   ]

This last definition turns out to be quite idiomatic using the Applicative interface of Gen. In essence, we specify that every time we generate a random Tree value, we do it by picking with uniform probability from a list of random generators using QuickCheck’s primitive function oneof :: [Gen a] -> Gen a. Each one of these sub-generators is specialized in generating a single constructor of our Tree data type. For instance, pure LeafA is a generator that always generates LeafAs, while Node <$> arbitrary <*> arbitrary is a generator that always produce Nodes, “filling” their recursive fields with random Tree values obtained by recursively calling our top-level generator.

As simple as this sounds, our Arbitrary Tree instance is able to produce the whole space of Tree values, which is really good, but also really bad! The problem is that Tree is a data type with an infinite number of values. Imagine picking Node constructors for every subterm, forever. You end up being stuck in an infinite generation loop, which is something we strongly want to avoid when using QuickCheck since, in principle, we want to test finite properties.

The “standard” solution to this problem is to define a “sized” generation process which ensures that we only generate finite values. Again, QuickCheck has a primitive for this called sized :: (Int -> Gen a) -> Gen a that let us define random generators parametrized over an Int value known as the generation size, which is an internal parameter of the Gen monad that is threaded on every recursive call to arbitrary, and that can be set by the user. Let’s see how to use it to improve our previous definition:

instance Arbitrary Tree where
 arbitrary = sized gen
   where
     gen 0 = oneof
       [ pure LeafA
       , pure LeafB
       ]
     gen n = oneof
       [ pure LeafA
       , pure LeafB
       , Node <$> gen (n-1) <*> gen (n-1)
       , Fork <$> gen (n-1) <*> gen (n-1) <*> gen (n-1)
       ]

In this previous definition we establish that, every time we generate a Tree value, we first obtain the current generation size by calling sized, and then we branch into two different generation processes based on it. In the case that we have a positive generation size (gen n), we proceed to choose between generating any Treeconstructor (just as we did before). The diference, however, is that we now reduce the generation size on every subsequent recursive call. This process repeats until we reach the base case (gen 0), where we resort on generating only terminal constructors, i.e., constructors without recursive arguments. This way we can ensure two interesting properties over the random values we generate:

1. They are always finite.
2. They have at most n levels, where n is the QuickCheck generation size set by the user.

The last property will be particulary useful in a couple of minutes, so keep it in mind.

Adding some flexibility to our generator

Right now we know how to write random generators for our custom data types using a type-driven fashion. This means that, to generate a value, we pick one of its constructors with uniform probability, and recursively generate its arguments with a progressively smaller generation size.

The problem with this approach is that choosing with uniform probability between constructors is usually not a good idea. Consider our last generator definition, one can easily see that half of the time we end up generating just leaves! Even so, the probability of generating a value with 10 level becomes 0.5¹⁰ = 0.00097 which is really small! This particular problem is highly dependent on the particular structure of the data type we want to generate, and gets worse as we increase the amount of terminal constructors present on it’s definition.

To solve this limitation, we can use QuickCheck’s function frequency :: [(Int, Gen a)] -> Gen a to pick a generator from a list of generators with an explicitly given frequency. Let’s see now how to rewrite our previous definition, parametrized by a given generation frequency fC for each constructor C:

instance Arbitrary Tree where
 arbitrary = sized gen
   where
     gen 0 = frequency
       [ (fLeafA, pure LeafA)
       , (fLeafB, pure LeafB)
       ]
     gen n = frequency
       [ (fLeafA, pure LeafA)
       , (fLeafB, pure LeafB)
       , (fNode,  Node <$> gen (n-1) <*> gen (n-1))
       , (fFork,  Fork <$> gen (n-1) <*> gen (n-1) <*> gen (n-1))
       ]

This last definition enables us to tweak the generation frequencies for each constructor and obtain different distributions of values in practice. So, the big question of this work is, how do we know how much the frequency of each constructor by itself affects the average distribution of values as a whole? Fortunately, there is an answer for this.

Branching processes

The key contribution of this work is to show that, if our generator follows some simple guidelines, then it’s possible to predict its average distribution of generated constructors very easily. To achieve this, we used a mathematical framework known as branching processes. A branching process is an special kind of stochastic model, and in particular, an special kind of Markov chain. They were originally conceived in the Victorian Era to predict the growth and extinction of the royal family names, and later spread to many other research fields like biology, physics, and why not, random testing.

Essentially, a branching process models the reproduction of individuals of different kinds across different time steps called generations, where it is assumed that the probability of each individual to procreate a certain individual in the next generation is fixed over time (this assumption is satisfied by our generator, since the generation frequencies for each constructor are hardcoded into the generator).

In our particular setting, we consider that each different data constructor constitutes an individual of its own kind. Then, during the generation process, each constructor will “produce” a certain average number of offpsring of possibly different kinds from one generation G_i to the next one (G_(i + 1)), i.e. from one level of the generated tree to the next one. Each generation G_i can be thought as a vector of natural numbers that groups the amount of generated constructors of each kind.

Then, by using branching processes theory, we can predict the expected distribution of constructors E[_] on each level of the generated tree or, in other words, the average number of constructors of each kind at every level of a generated value. Then, E[G_i] is a vector of real numbers that groups the average amount of generated constructors of each kind at the i-th level.

On the other hand, given a generation size n, we know that our generation process will produce values of up to nlevels of depth. Therefore we can ensure that the generation process encoded by a branching process will take place from the first generation (G₀), up to the (n − 1)-th generation G_{(n − 1)}, while the last generation (G_n) is only intended to fill the recursive holes produced by the recursive constructors generated in the previous generation G_{(n − 1)}, and needs to be considered separately.

With these considerations, we can characterize the expected distribution of constructors of any value generated using a QuickCheck size n. We only need to add the expected distribution of constructors at every level of the generated value, plus the terminal constructors needed to terminate the generation process at the last level.

Hopefully, the next figure gives some insights on how to predict the expected distribution of constructors of a Tree value randomly generated using our previously generator.

There you can see that the generation process consists of two different random processes, one corresponding to each clause of the auxiliary function gen that we defined before. We need to calculate them separately in order to be sound with respect to our generator.

What about complex data types?

The example I have shown you may not convice you at all about our prediction mechanism given that it’s fairly simple. However, in our paper we show that it is powerful enough to deal with complex data types comprising for instance, composite types, i.e. data types defined using other types internally; as well as mutually recursive data types. For simplicity, I will not explain the details about them in this post, but you can find them in the paper if you’re still unconvinced!

DRAGEN: automatic Derivation of RAndom GENerators

One of the cool things about being able to predict the distribution of data constructors is that we can use this prediction as optimization feedback, allowing us to tune the generation probabilities of each constructor without actually generating a single value. To do so, we implemented a Haskell tool called DRAGEN that automatically derives random generators in compile-time for the data types we want, using the branching processes model I’ve previously introduced to predict and tune the generation probabilities of each constructor. This way, the user expresses a desired distribution of constructors, and DRAGEN tries to satisfy it as much as possible while deriving a random generator.

DRAGEN works at compile-time exploiting Template Haskell meta-programming capabilities, so the first step to use it is to enable the Template Haskell language extension and import it:

{-# LANGUAGE TemplateHaskell #-}

import Dragen

Then, we can use DRAGEN to automatically derive a generator for our Tree data type very easily with the following Template Haskell function:

dragenArbitrary :: Name -> Size -> DistFunction -> Q [Dec]

Where Name is the name of the data type you want to derive a generator for, Size is the maximum depth you want for the generated values (Size is a type synonym of Int), and DistFunction is a function that encodes the desired distribution of constructors as a “distance” to a certain target distribution. Let’s pay some attention to its definition:

type DistFunction = Size -> FreqMap -> Double
type FreqMap = Map Name Int

This is, for every generation size and mapping between constructor names and generation frequencies, we will obtain a real number that encodes the distance between the predicted distribution using such values, and the distribution that we ideally want. Hence, our optimization process works by minimizing the output of the provided distance function. On each step, it varies the generation frequencies of each constructor independently, following the shortest path to the desired distribution. This process is repeated recursively until it reachs a local minimum, where we finally synthesize the required generator code using the frequencies found by it.

Fortunately, you don’t have to worry too much about distance functions in practice. For this, DRAGEN provides a minimal set of distance functions that can be used out of the box. All of them are built around the Chi-Squared goodness of fit test, an statistical test useful to quantify how much a set of observed frequencies differs from an expected one. In our case, the observed frequencies corresponds to the predicted distributions of constructors, while the expected ones corresponds to the target distribution of constructors. Let’s see some of them in detail!

Uniform generation

The simplest distance function provided by DRAGEN is uniform :: DistFunction, which guides the frequencies optimization process towards a distribution of constructors where the amount of generated constructors for every constructor is (ideally) equal to the generation size. In mathematical jargon, it looks a bit like:

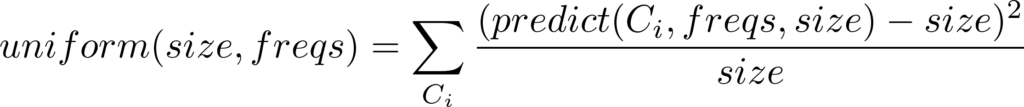
Where C_i varies among all the data constructors involved in the generation process.

For instance, if we write this declaration at the top level of our code:

dragenArbitrary ''Tree 10 uniform

Then DRAGEN will produce the following code in compile-time:

Reifiying: Tree

Types involved with Tree:
[Base Tree]

Initial frequencies map:
 * (Fork,100)
 * (LeafA,100)
 * (LeafB,100)
 * (Node,100)

Predicted distribution for the initial frequencies map:
 * (Fork,8.313225746154785)
 * (LeafA,12.969838619232178)
 * (LeafB,12.969838619232178)
 * (Node,8.313225746154785)

Optimizing the frequencies map:
********************************************************************************
********************************************************************************
*******************************************************************

Optimized frequencies map:
 * (Fork,152)
 * (LeafA,165)
 * (LeafB,162)
 * (Node,175)

Predicted distribution for the optimized frequencies map:
 * (Fork,7.0830066259820645)
 * (LeafA,11.767371412451563)
 * (LeafB,11.553419204952444)
 * (Node,8.154777365439879)

Initial distance: 2.3330297615435938
Final distance: 1.7450409851023654
Optimization ratio: 1.3369484049148201

Deriving optimized generator...

Splicing declarations
    dragenArbitrary ''Tree 10 uniform
  ======>
    instance Arbitrary Tree where
      arbitrary
        = sized go_arOq
        where
            go_arOq n_arOr
              = if (n_arOr == 0) then
                    frequency [(165, return LeafA), (162, return LeafB)]
                else
                    frequency
                      [(165, return LeafA), (162, return LeafB),
                       (175,
                        Node <$> go_arOq ((max 0) (n_arOr - 1))
                          <*> go_arOq ((max 0) (n_arOr - 1))),
                       (152,
                        Fork <$> go_arOq ((max 0) (n_arOr - 1))
                          <*> go_arOq ((max 0) (n_arOr - 1))
                          <*> go_arOq ((max 0) (n_arOr - 1)))]

As you can see, the optimization process tries to reduce the difference between the predicted number of generated constructors for each constructor, and the generation size (10 in this case). Note that this process is far from perfect in this case and, in fact, we cannot expect exact results in most cases. The reason for the observable differences between the obtained distribution and the desired one due to the implicit invariants of our Tree data type. So, it’s important to be aware that most data types carry implicit invariants with them that we can’t break while generating random values. For example, trying to obtain a uniform distribution of constructors for a lists [] data type makes no sense, since we will always generate only one “nil” per list.

After deriving a random generator using our tool, you’d likely be interested in confirming that the predictions we made over the constructors distributions are sound. For this, our tool provides a function confirm :: Countable a => Size -> Gen a -> IO () to do so:

ghci> confirm 10 (arbitrary :: Gen Tree)
 * ("Fork",7.077544)
 * ("LeafA",11.757322)
 * ("LeafB",11.546111)
 * ("Node",8.148345)

Where the constraint Countable a can be automatically satisfied providing a Generic instance of a, and in our case we can simply use standalone deriving to obtain it:

{-# LANGUAGE DeriveGeneric  #-}
{-# LANGUAGE StandaloneDeriving #-}

deriving instance Generic Tree
instance Countable Tree

Weighted generation

There may be some scenarios when we know that some constructors are more important that some other ones while testing. In consequence, our tool provides the distance function weighted :: [(Name, Int)] -> DistFunction to guide the optimization process towards a target distribution of constructors where some of them can be generated in different proportion than some other ones.

Using this distance function, the user lists the constructors and proportions of interest, and the optimization process will try to minimize the following function:

Note that we only consider the listed constructors to be relevant while calculating the distance to the target distribution, meaning that the optimizator can freely adjust the rest of them in order to satisfy the constraints impossed in the weights list.

For instance, say that we want to generate Tree values with two LeafAs for every three Nodes, we can express this in DRAGEN as follows:

dragenArbitrary ''Tree 10 (weighted [(2, 'LeafA), (3, 'Node)])

Obtaining:

Reifiying: Tree

...

Optimizing the frequencies map:
********************************************************************************
***************************************

Optimized frequencies map:
 * (Fork,98)
 * (LeafA,32)
 * (LeafB,107)
 * (Node,103)

Predicted distribution for the optimized frequencies map:
 * (Fork,28.36206776375821)
 * (LeafA,20.15153900775499)
 * (LeafB,67.38170855718076)
 * (Node,29.809112037419343)

Initial distance: 18.14836436989009
Final distance: 2.3628106855081705e-3
Optimization ratio: 7680.837267750427

Deriving optimized generator...
...

Note in the previous example how the generation frequencies for LeafB and Fork are adjusted in a way that the specified proportion for LeafA and Node can be satisfied.

Whitelisting/blacklisting constructors

Many testing scenarios would require to restrict the set of generated constructors to some subset of the available ones. We can express this in DRAGEN using the functions only :: [Name] -> DistFunction and without :: [Name] -> DistFunction to whitelist and blacklist some constructors in the derived generator, respectively. Mathematically:

Is worth noticing that, in both distance functions, the restricted subset of constructors is then generated following a uniform fashion. Let’s see an example of this:

dragenArbitrary ''Tree 10 (only ['LeafA, 'Node])

Which produces:

Reifiying: Tree

...

Optimizing the frequencies map:
********************************************************************************
****************************************************************

Optimized frequencies map:
 * (Fork,0)
 * (LeafA,158)
 * (LeafB,0)
 * (Node,199)

Predicted distribution for the optimized frequencies map:
 * (Fork,0.0)
 * (LeafA,10.54154398815233)
 * (LeafB,0.0)
 * (Node,9.541543988152332)

Initial distance: 2.3732602211951874e7
Final distance: 5.036518059032003e-2
Optimization ratio: 4.7121050562684125e8

Deriving optimized generator...
...

In this last example we can easily note an invariant constraining the optimization process: every binary tree (which is how we have restricted our original Tree) with n nodes has exactly n + 1 leaves. Considering this, the best result we can obtain while optimizing the generation frequencies consists of generating an average number of nodes and leaves that are simetric on its distance to the generation size.

Try DRAGEN!

DRAGEN is now in Hackage! I would love to hear some feedback about it, so feel free to open an issue in GitHub or to reach me by email whenever you want!